Zadání 3. kola matematického korespondenčního semináře 2006/2007
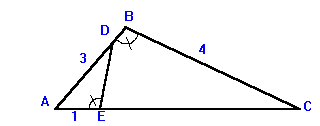
1. V trojúhelníku ABC na obrázku platí: úhel ABC je shodný s úhlem DEA. Délka strany AB je 3, délka strany BC je 4, úsek AE má velikost 1. Určete délku úsečky ED.
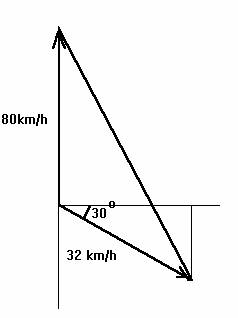
- Motorový člun má zásoby paliva na 4 hodiny, opouští loď a míří přesně na sever rychlostí 80 km/h. Loď pokračuje 30° jihovýchodně (podle obrázku) rychlostí 32 km/h. Určete maximální možnou vzdálenost, kterou člun může severně ujet, aby se bezpečně stihl vrátit k lodi, kde opět načerpá palivo (předpokládejme, že člun se vrací po přímce).
Návod k řešení: použijte např. kosinovou větu.
- Na narozeninové oslavě se rozdávaly bonbóny. Nejdříve si vzal Karel jeden kus. Potom si vzal Jirka dva kusy. Každý další si vzal vždy o jeden kus víc než jeho předchůdce. Potom se všichni rozdělili mezi sebou rovným dílem.. Kolik lidí bylo na oslavě, jestliže každý získal 6 kusů?
- Horáčkovi snídají 10 topinek. Na pánev se vejdou najednou právě dvě topinky. Každou stranu topinky je třeba smažit 20 vteřin. Určete nejkratší možnou dobu, která je potřebná k osmažení všech topinek.
- Co to je Eulerova přímka?
Řešení zasílejte do 27. dubna 2007 na adresu:
kabinet matematiky, gymnázium Jírovcova 8, České Budějovice, 371 61