Zadání úloh 2. kola korespondenčního matematického semináře 2008/09
- Za přistavení nebo vyzvednutí vozidla mimo Prahu účtuje autopůjčovna CAR pevný poplatek 200 Kč plus 4 Kč za každý kilometr. Za tytéž služby účtuje autopůjčovna RENTAL pevný poplatek 300 Kč plus 3 Kč za každý kilometr. Při jaké vzdálenosti je stejně výhodné vypůjčení auta od CAR i RENTAL, jsou-li ostatní služby zpoplatněny stejně?
Úlohu řešte a) výpočtem
b) graficky.
- Vytvořte pravidelný mnohostěn ze šesti stejných zápalek, aniž byste je lámali. Řešení
 narýsujte.
narýsujte.
- Najděte desetinné číslo x z intervalu < 1,9 >, jehož čtyřnásobek se rovná součtu jeho cifer.Uveďte všechna řešení.
[Nápověda: Najděte libovolné desetinné číslo y z intervalu < 1,9 >, jehož osminásobek se rovná součtu jeho cifer.
Řešení nápovědy: hledané číslo y = 1,125 (součet cifer čísla 1,125 je 1+1+2+5 = 9, jeho osminásobek je 1,125*8 = 9) ]
- Dva chodci se k sobě stále přibližují. Jejich vzdálenost je 9 km a jeden z nich jde dvakrát rychleji než druhý. Víme, že se potkají za hodinu. Mezi nimi pobíhá jejich pes průměrnou rychlostí 10 km za hodinu, a to tak, že na začátku vyběhne od rychlejšího k pomalejšímu a až se k němu dostane, ihned se otočí k rychlejšímu a tak dál, dokud se oba chodci nepotkají. Pak pes zůstane sedět. Kolik kilometrů pes naběhá, než se oba chodci potkají?
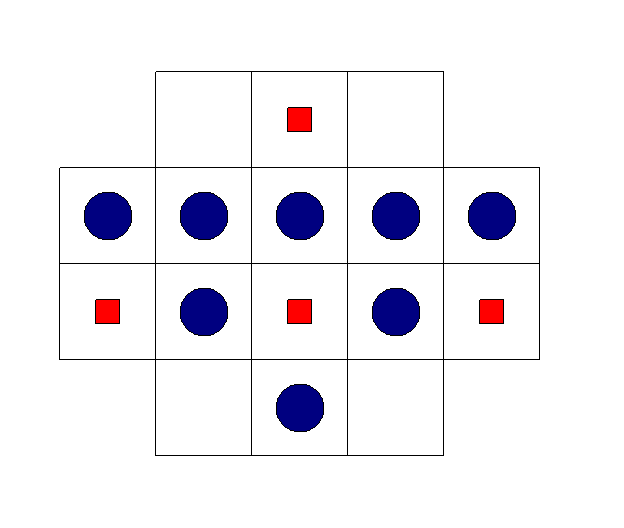
- Rozdělte plánek( na následující stránce) na 4 díly shodné tvarem a velikostí, z nichž každý bude obsahovat 2 kolečka, jeden čtvereček a jedno prázdné místo.
Řešení zasílejte do 15. ledna 2009 na adresu:
kabinet matematiky, gymnázium Jírovcova 8, České Budějovice, 371 61
nebo na e-mail: trca@gymji.cz
(Řešení, je třeba zasílat jako přílohu ve formě jednoho textového souboru s případnými vloženými obrázky (tj. jeden soubor celkem)).